RED NEURONAL PERCEPTRON (Clasificador Lineal)
Antecedentes. La primera red neuronal conocida, fue desarrollada en 1943 por Warren McCulloch y Walter Pitts; ésta consistía en una suma de las señales de entrada, multiplicadas por unos valores de pesos escogidos aleatoriamente. La entrada es comparada con un patrón preestablecido para determinar la salida de la red. Si en la comparación, la suma de las entradas multiplicadas por los pesos es mayor o igual que el patrón preestablecido la salida de la red es uno (1), en caso contrario la salida es cero (0). Al inicio del desarrollo de los sistemas de inteligencia artificial, se encontró gran similitud entre su comportamiento y el de los sistemas biológicos y en principio se creyó que este modelo podía computar cualquier función aritmética o lógica.
La red tipo Perceptrón fue inventada por el psicólogo Frank Rosenblatt en el año 1957. Su intención era ilustrar algunas propiedades fundamentales de los sistemas inteligentes en general, sin entrar en mayores detalles con respecto a condiciones específicas y desconocidas para organismos biológicos concretos.
El Perceptrón era inicialmente un dispositivo de aprendizaje, en su configuración inicial no estaba en capacidad de distinguir patrones de entrada muy complejos, sin embargo mediante un proceso de aprendizaje era capaz de adquirir esta capacidad.
Estructura de la red.
La estructura de un Perceptrón sencillo; en la que se observa la adición de una condición umbral en la salida. Si la entrada neta, a esta condición es mayor que el valor umbral, la salida de la red es 1, en caso contrario es 0 (ó -1).
Veamos mediante el siguiente gráfico la estructura de la perceptron:
Regla de aprendizaje.El Perceptrón es un tipo de red de aprendizaje supervisado, es decir necesita conocer los valores esperados para cada una de las entradas presentadas; su comportamiento está definido por pares de esta forma:
{p1, t1 },{p2 , t2 }, . . . ,{pQ , tQ }
Cuando p es aplicado a la red, la salida de la red es comparada con el valor esperado t, y la salida de la red esta determinada por una función de salida, como las que se muestran a continuación:

Perceptron para Clasificar Nueces, utilizando el Algoritmo de Aprendizaje para el Perceptron y
Bueno en aquí hemos implementado el Algoritmo Perceptrón con su Algoritmo de Aprendizaje y el algoritmo Perceptrón en su forma primal.
Para el Algoritmo Perceptrón con su Algoritmo de Aprendizaje (como para el Adeline), se utilizaron los siguiente patrones de entrada y de salida deseada, tanto para el AND como para las nueces:
- Patrones entrenamiento para AND
Patrones de Entrada:
X1= [1.0 , 1.0 , 1.0]
X2= [1.0 , 1.0 , -1.0]
X3= [1.0 , -1.0 , 1.0]
X4= [1.0 , -1.0 , -1.0]
Patrones de Salida:
D1= 1.0
D2= -1.0
D3= -1.0
D4= -1.0
- Patrones entrenamiento para Nueces

Es decir:
Patrones de Entrada:
X1= [1.0 , 2.2 , 1.4]
X2= [1.0 , 1.5 , 1.0]
X3= [1.0 , 0.6 , 0.5]
X4= [1.0 , 2.3 , 2.0]
X5= [1.0 , 1.3 , 1.5]
X6= [1.0 , 0.3 , 1.0]
Patrones de Salida:
D1= 1.0
D2= 1.0
D3= 1.0
D4= -1.0
D5= -1.0
D6= -1.0
Para el Algoritmo Perceptrón Primal (como para el Dual), se utilizaron los siguiente patrones de entrada y de salida deseada, tanto para el AND como para las nueces:
- Patrones entrenamiento para AND
Patrones de Entrada:
X1= [1.0 , 1.0]
X2= [1.0 , -1.0]
X3= [-1.0 , 1.0]
X4= [-1.0 , -1.0]
Patrones de Salida:
D1= 1.0
D2= -1.0
D3= -1.0
D4= -1.0
- Patrones entrenamiento para Nueces
Patrones de Entrada:
X1= [2.2 , 1.4]
X2= [1.5 , 1.0]
X3= [0.6 , 0.5]
X4= [2.3 , 2.0]
X5= [1.3 , 1.5]
X6= [0.3 , 1.0]
Patrones de Salida:
D1= 1.0
D2= 1.0
D3= 1.0
D4= -1.0
D5= -1.0
D6= -1.0

A continuación algunos experimentos realizados:
PERCEPTRÓN NUECES Factor de Aprendizaje: 0.15
• Matriz de Pesos Inicial:
peso [0]= 0.12589034468012628
peso [1]= 0.7903058923898821
peso [2]= 0.9984030903113681
• Matriz de Pesos:
peso [0]= 0.12589034468012628
peso [1]= 0.3703058923898827
peso [2]= -0.5615969096886317
• Numero de Iteraciones:9
Factor de Aprendizaje: 0.2
• Matriz de Pesos Inicial:
peso [0]= 0.5211053777949533
peso [1]= 0.2648711912609053
peso [2]= 0.9012579714386163
• Matriz de Pesos:
peso [0]= 0.5211053777949533
peso [1]= 0.4248711912609069
peso [2]= -1.0187420285613844
• Numero de Iteraciones: 10
Factor de Aprendizaje: 0.25
• Matriz de Pesos Inicial:
peso [0]= 0.4635237244427848
peso [1]= 0.811524746560602
peso [2]= 0.6304562017839236
• Matriz de Pesos:
peso [0]= 0.9635237244427848
peso [1]= 1.3115247465606044
peso [2]= -2.269543798216076
• Numero de Iteraciones: 15
PERCEPTRÓN AND Factor de Aprendizaje: 0.15
• Matriz de Pesos Inicial:
peso [0]= 0.49061731276640874
peso [1]= 0.006799938954024531
peso [2]= 0.3200514432209699
• Matriz de Pesos:
peso [0]= -0.4093826872335912
peso [1]= 0.3067999389540245
peso [2]= 0.6200514432209698
• Numero de Iteraciones: 4
Factor de Aprendizaje: 0.2
• Matriz de Pesos Inicial:
peso [0]= 0.3492676171883031
peso [1]= 0.5332770227376556
peso [2]= 0.44576721981941836
• Matriz de Pesos:
peso [0]= -0.4507323828116969
peso [1]= 0.5332770227376556
peso [2]= 0.44576721981941836
• Numero de Iteraciones: 2
Factor de Aprendizaje: 0.25
• Matriz de Pesos Inicial:
peso [0]= 0.6058080756193948
peso [1]= 0.6177095431809719
peso [2]= 0.8570807155227276
• Matriz de Pesos:
peso [0]= -0.39419192438060524
peso [1]= 0.6177095431809719
peso [2]= 0.8570807155227276
• Numero de Iteraciones: 2
PRIMAL AND Factor de Aprendizaje: 0.15
• Matriz de Pesos Inicial:
peso [0]=0.04337321278786277
peso [1]=0.8707094307946116
peso [2]=0.8313040363776814
• Matriz de Pesos:
peso [0]=-0.10662678721213723
peso [1]=0.7207094307946116
peso [2]=0.9813040363776814
• Valor de b: -0.4499999999999999
• Valor de k: 1
• Numero de Iteraciones: 2
Factor de Aprendizaje: 0.2
• Matriz de Pesos Inicial:
peso [0]=0.18526642378180813
peso [1]=0.8435329132210375
peso [2]=0.2543760126900195
• Matriz de Pesos:
peso [0]=-0.01473357621819188
peso [1]=0.6435329132210375
peso [2]=0.45437601269001954
• Valor de b: -0.6
• Valor de k:1
• Numero de Iteraciones: 2
Factor de Aprendizaje: 0.25
• Matriz de Pesos Inicial:
peso [0]=0.906910074177728
peso [1]=0.2607305274667093
peso [2]=0.7652212917544058
• Matriz de Pesos:
peso [0]=0.40691007417772795
peso [1]=0.7607305274667093
peso [2]=0.7652212917544059
• Valor de b: -1.4999999999999998
• Valor de k: 4
• Numero de Iteraciones: 3
Ejecutándolo el algoritmo Perceptrón Primal, para el primer caso, cuando el factor de aprendizaje = 0.1, tenemos:
De los 4 patrones de entrada se escoge el de max(R) = 1.7320508075688772
Para i = 0
entrada = [1.0 , 1.0 , 1.0]
Si ( 1.6260213167230448 < = 0 ) -> falso
Matriz de Pesos:
• peso [0]= 0.6179109054594774
• peso [1]= 0.5502077938601178
• peso [2]= 0.4579026174034496
Valor de b = 0.0
Valor de k = 0
Para i = 1
entrada = [1.0 , 1.0 , -1.0 ]
Si ( -0.7102160819161455 < = 0 ) entonces
Matriz de Pesos:
• peso [0]= 0.5179109054594774
• peso [1]= 0.4502077938601178
• peso [2]= 0.5579026174034496
Valor de b = -0.3
Valor de k = 1
Para i = 2
entrada = [ 1.0 , -1.0 , 1.0 ]
Si ( -0.3256057290028092 < = 0) entonces
Matriz de Pesos :
• peso [0]= 0.4179109054594774
• peso [1]= 0.5502077938601178
• peso [2]= 0.4579026174034496
Valor de b = -0.6
Valor de k = 2
Para i = 3
entrada = [ 1.0 , -1.0 , -1.0 ]
Si ( 1.19019950580409 < = 0 ) -> falso
Matriz de Pesos:
• peso [0]= 0.4179109054594774
• peso [1]= 0.5502077938601178
• peso [2]= 0.4579026174034496
Valor de b = -0.6
Valor de k = 2
Otra iteración Para i = 0
entrada = [ 1.0 , 1.0 , 1.0 ]
Si ( 0.8260213167230447 < = 0 ) -> falso
Matriz de Pesos:
• peso [0]= 0.4179109054594774
• peso [1]= 0.5502077938601178
• peso [2]=0.4579026174034496
Valor de b = -0.6
Valor de k = 2
Para i = 1
entrada = [ 1.0 , 1.0 , -1.0 ]
Si ( 0.08978391808385444 < = 0 ) -> falso
Matriz de Pesos
• peso [0]= 0.4179109054594774
• peso [1]= 0.5502077938601178
• peso [2]= 0.4579026174034496
Valor de b = -0.6
Valor de k = 2
Para i = 2
entrada = [ 1.0 , -1.0 , 1.0 ]
Si ( 0.2743942709971907 < = 0 ) -> falso
Matriz de Pesos
• peso [0]= 0.4179109054594774
• peso [1]= 0.5502077938601178
• peso [2]= 0.4579026174034496
Valor de b = -0.6
Valor de k = 2
Para i = 3
entrada = [ 1.0 , -1.0 , -1.0 ]
Si ( 1.19019950580409 < = 0 ) -> falso
Matriz de Pesos
• peso [0]= 0.4179109054594774
• peso [1]= 0.5502077938601178
• peso [2]= 0.4579026174034496
Valor de b = -0.6
Valor de k = 2
Entonces el numero de iteraciones del primal es:2













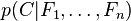
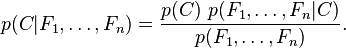


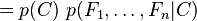

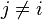 . Esto significa que
. Esto significa que 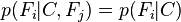
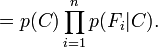
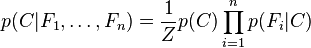
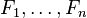 , es decir, constante si los valores de
, es decir, constante si los valores de 





























