TOPICO: Inteligencia Artificial: Laboratorio 3

Busqueda Informada

Implementar busqueda A* para solucionar el problema del 8 puzzle utilizando h1 y h2 vistos en clase
Implementar RBFS y probarlo para encontrar la ruta mas corta de un punto A hacia uno B
Implementar el algoritmo Hill climbing para solucionar el TSP y el problema de las 8 reynas
Cuestionario de capitulo 3 y 4 de RUSSELL, Stuart and NORVIG, Peter Artificial Intelligence a Modern Aproach, second edition 2003.
Pruebas realizadas a los algoritmos antes mencionados, el documento integro se puede descargar de aquí.

Similar que para el laboratorio, los algoritmos para los problemas propuestos, fueron desarrollados en DrScheme, a excepción del Problema de la 8-reynas, que fue implementado en Matlab. A continuación una breve descripción de ellas:

La implementación del A* es similar a los de Búsqueda No informada ya desarrollada y mencionadas en Laboratorio 1.

Con la diferencia que fueron añadidas el calcular las heurísticas, h(n) vistas en clase, que son: El número de fichas fuera de sus posiciones entre el estado actual y el meta, y el número de pasos que hay que hacer para llegar mover una pieza hasta la posición del estado meta. Y a la vez modificando la estructura nodo, ya que para el caso de la búsqueda A* tenemos la heurística dada asi:
f(n) = g(n) + h(n),
donde g(n) viene a ser costo desde el estado inicial al estado siendo evaluado, y el h(n), que es la heurística desde el estado actual hacia el estado meta u objetivo.

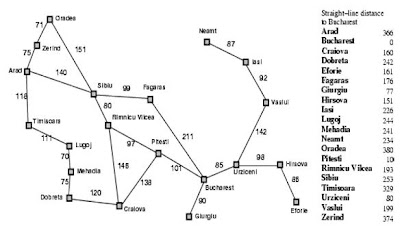
Busqueda RBFS aplicado al mapa de Romania (con 20 ciudades) para encontrar la ruta más corta entre una ciudad A y B

Implementamos dos casos, uno para el caso en que de todas las ciudades llegan a bucharest (como el dado en Clase y libro de Russell) y usando las distancias en linea recta (para la heurísticas) las mismas dadas, y otro suponiendo que cada ciudad tiene unas ciertas posiciones (X,Y), para calcular las distancias en linea recta, como:

arad --- (91 , 492)
bucharest --- (400 , 327)
craiova --- (253 , 288)
dobreta --- (165 , 299)
eforie --- (562 , 293)
fagaras --- (305 , 449)
giurgiu --- (375 , 270)
hirsova --- (534 , 350)
iasi --- (473 , 506)
lugoj --- (165 , 379)
mehadia --- (168 , 339)
neamt --- (406 , 537)
oradea --- (131 , 571)
pitesti --- (320 , 368)
rimnicu --- (233 , 410)
sibiu --- (207 , 457)
timisoara --- (94 , 410)
urziceni --- (456 , 350)
vaslui --- (509 , 444)
zerind --- (108 , 531)

A continuación algunas muestras de pantalla de la interfaz, seleccionando una ciudad, ejecutando el algoritmo y los resultados obtenidos:

Búsqueda Greedy aplicado al Problema del TSP

Implementamos una búsqueda Greedy para la solución al TSP (Travel SalesPerson - Agente Viajero), donde dado 20 ciudades (del Mapa de Romania), y dado un punto de partida, escoge la mejor ruta posible (la más optima, menor Costo) para visitar a todas sin pasar por la misma ciudad 2 veces. A continuación se muestra el proceso de eligir una ciudad de inicio, en la interfaz:

Búsqueda Hill Climbing aplicado al Problema del TSP

Implementamos la Búsqueda Hill Climbing al Problema del TSP ya mencionado, pero para este caso se consideraron sólo 12 ciudades, de las 20 ya mencionadas, y éstas son:

arad --- (91 , 492)
bucharest --- (400 , 327)
craiova --- (253 , 288)
eforie --- (562 , 293)
fagaras --- (305 , 449)
neamt --- (406 , 537)
oradea --- (131 , 571)
pitesti --- (320 , 368)
sibiu --- (207 , 457)
timisoara --- (94 , 410)
vaslui --- (509 , 444)
zerind --- (108 , 531)

Veamos la interfaz de la aplicación:

Donde luego de pulsar el boton Ejecutar, se procederá a escoger una ruta aleatoria, la misma que es mostrada en Inicio, luego se ejecutará la Búsqueda Hill Climbing, y se mostrará el numero de rutas posibles (camino) y las mismas que se consideraron para llegar a la solución final, y por ultimo la solución final obtenida, ejemplo véase la siguiente figura:

Búsqueda Hill Climbing aplicado al Problema de las 8-reynas

Esta búsqueda fue implementada en Matlab, donde se trató que dada una configuración inicial de las reynas, éstas se posicionen de tal forma que no se ataquen directamente o indirectamente entre pares de reynas, como sabemos las reynas se atacan en forma vertical, horizontal y diagonal. Se busca las posiciones más optimas y esto se puede observar al obtener como h(n), es decir número de par de reinas atacándose, igual a "0" o cercano a él como: "1".

Los algoritmos usados para determinar el nº de colisiones de reinas fueron recopilados de Algoritmos para el problema de las n-reinas .

Cuestionario de capitulo 3 y 4 de RUSSELL, Stuart and NORVIG, Peter Artificial Intelligence a Modern Aproach, second edition 2003.

Bueno las respuestas a este cuestionario, se encuentran en el link ya presentado al inicio de este Post, sin embargo aquí mencionaremos algunas de ellas.

3.1. Defina con sus propias palabras los siguientes términos: estado, espacio de estados, árbol de búsqueda, nodo de búsqueda, objetivo, acción, función sucesor y factor de ramificación.

Estado: es una representación que toma un agente, dado alguna acción (nulo si es estado inicial).
Espacio de Estados: está conformado por un conjunto de todos los estados alcanzables desde el estado inicial, generados dado una determinada acción.
Árbol de Búsqueda: dado por la abstracción o representación del espacio de estados.
Nodo de Búsqueda: es un determinado estado representado en un árbol de búsqueda.
Objetivo: es algo abstracto que representa a donde quiero llegar.
Acción: es el acto de responder ante una determinada situación o estado, para así poder obtener otros nuevos estados.
Función Sucesor: función que describe las posibles acciones que puede realizar el agente y los estados resultantes a dichas acciones. Es decir, función que devuelve una lista de pares: (acción, sucesor).
Factor de Ramificación: número máximo de sucesores que se pueden obtener aplicando la Función Sucesor a un determinado estado

3.2. Explique porqué la formulación del problema debe seguir a la formulación del objetivo.

La formulación del problema debe seguir a la formulación del objetivo porque de lo que trata la formulación del objetivo es de decidir en que aspectos del mundo estamos interesados, e ignorar el resto en el proceso de abstracción. Por otro lado en la formulación del problema lo que hacemos es decidir como manipular aquellos aspectos relevantes (es decir los de la formulación del objetivo) e ignorar el resto. Entonces por ende si nosotros escogemos realizar primero la formulación del problema no sabremos que aspectos considerar y que no.

4.1. Trace cómo opera la búsqueda A* aplicada al problema de alcanzar Bucharest desde Lugoj, utilizando la heurística distancia en línea recta. Es decir muestre la secuencia de nodos que considerará el algoritmo y los valores f, g y h para cada nodo.
Nota: f(n)=g(n) + h(n), (se recomienda que se accese al domumento .pdf, para poder observar mejor las siguientes imágenes, ya que debido a la estructura de este post, hay deficiencias para poder observar bien las imagenes :D)

4.2. El algoritmo de camino heurístico es uan búsqueda primero el mejor en la cual la función objetivo es f(n) = (2 - w)g(n) + wh(n). ¿Para qué valores de w, está garantizado que el algoritmo sea óptimo? ¿Qué tipo de búsqueda realiza cuando w=0? ¿cuando w=? ¿cuando w=2?

Tenemos la función objetivo: f(n) = (2 - w)g(n) + wh(n),
Entonces para hallar los valores de w en el cual sea óptimo el algoritmo hacemos que cumpla:

f(n) = (2 - w)g(n) + wh(n) <= g(n) + h(n) -> 2g(n) – wg(n) + wh(n) <= g(n) + h(n) -> g(n) – wg(n) + wh(n) – h(n) <= 0 -> - g(n) (w - 1) + h(n)( w – 1) <= 0 -> (w - 1) (- g(n) + h(n)) <= 0 -> w – 1 <= 0 -> w <= 1 Ahora para el caso de:

w = 0, nos queda: f(n) = 2g(n); la cual el tipo de búsqueda que puede utilizar esta función objetivo es la Búsqueda de Costo Uniforme, ya que el factor de 2, no altera o no hace nada relevante en el orden de los nodos.
w = 1, nos queda: f(n) = g(n) + h(n); la cual el tipo de búsqueda que utiliza esta función objetivo es la Búsqueda A*
w = 2, nos queda: f(n) = 2h(n); la cual el tipo de búsqueda que utiliza esta función objetivo es la Búsqueda Greedy Primero el Mejor.