
Clasificador de SPAM y NO SPAM
Antes de comentar la aplicación en si veamos algo de teoría. Un clasificador Bayesiano "naïve" es una clasificador probabilístico que se basa en aplicar el Teorema de Bayes. Este tipo de clasificadores es frecuentemente empleado para detectar mensajes de correo basura (spam).
En abstracto, el modelo de probabilidad para un clasificador es
sobre una variable dependiente C, con un pequeño número de resultados (o clases). Esta variable está condicionada por varias variables independientes desde F1 a Fn. El problema es que si el número n de variables independientes es grande (o cuando éstas pueden tomar muchos valores), entonces basar este modelo en tablas de probabilidad se vuelve imposible. Por lo tanto el modelo se reformula para hacerlo más manejable:
Usando el teorema de Bayes se escribe:
Lo anterior podría reescribirse en lenguaje común como:
En la práctica sólo importa el numerador, ya que el denominador no depende de C y los valores de Fi son datos, por lo que el denominador es, en la práctica, constante.
El numerador es equivalente a una probabilidad compuesta:
que puede ser reescrita como sigue, aplicando repetidamente la definición de probabilidad condicional:
... y así sucesivamente. Ahora es cuando la asunción "naïve" de independencia condicional entra en juego: se asume que cada Fi es independiente de cualquier otra Fj para
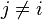 . Esto significa que
. Esto significa que por lo que la probabilidad compuesta puede expresarse como
Esto significa que haciendo estas asunciones, la distribución condicional sobre la variable clasificaroria C puede expresarse de la siguiente manera:
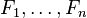 , es decir, constante si los valores de Fi son conocidos
, es decir, constante si los valores de Fi son conocidosAhora con el conocimiento previo comentemos la aplicación

El presente programa usa el algoritmo de Naive Bayes para clasificar mensajes de correo y determinar si estos son SPAM o NO SPAM.
Para construir el programa, hemos empleado una cierta cantidad de mensajes de prueba los cuales hemos clasificado manualmente en SPAM o NO SPAM. Para cada mensaje de prueba son eliminadas las palabras, por ejemplo:”la, lo, del, sobre, encima, y, o, etc” y así asociaremos ciertas palabras al hecho que el mensaje sea SPAM o NO SPAM. Se recomienda también transformar los verbos infinitivos y las plurales a singular.
Los mensajes de prueba son la base del algoritmo empleado y ayudaran a determinar si un nuevo mensaje pertenece a la clase SPAM o NO SPAM, teniendo en cuenta la clase que tenga mayor probabilidad de pertenencia.
El grado de pertenencia se determinara de acuerdo a la mayor cantidad de palabras que concuerden con el texto nuevo ya sean de clase SPAM o NO SPAM.
En el presente envió se adjuntan los archivos de entrenamiento y los de prueba, descargar aquí.
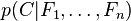
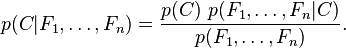


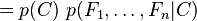

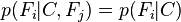
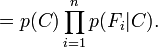
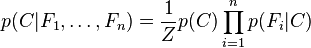





No comments:
Post a Comment